Estadística Inferencial

         
                                                               
                                                             PRESENTACIÓN 

• Apellidos :Chahuillco Caceres ,Medallyt
• Facultad :Ciencias Sociales 
• Escuela Académica Profesional : EAP Trabajo Social 
• Curso :Estadística Social II
• Profesor :Demetrio Ccesa Rayme 
• Tema:Estadistica Inferencial
•  Ciclo :cuarto 

                                          2015







                             UNIVERSIDAD NACIONAL FEDERICO VILLARREAL 
   

VISIÓN :

La Universidad Nacional Federico Villarreal" será una comunidad académica acreditada bajo estándares globales de calidad, posicionada internacionalmente, y al servicio del desarrollo humano sostenible.

MISIÓN:
"La Universidad Nacional Federico Villarreal" tiene por misión, la formación de la persona humana, y el fortalecimiento de la identidad cultural de la nación, fundado con el conocimiento científico y tecnológico, en correspondencia con el desarrollo humano sostenible. 


                                      FACULTAD CIENCIAS SOCIALES 

MISIÓN :

La nueva Facultad de Ciencias Sociales concibe su desarrollo académico en el ámbito general de tres grandes misiones: La Formativa, La de Investigación y De Apoyo a la Gestión; Aplicada conjuntamente en las tres escuelas profesionales: Sociología, Trabajo Social y Ciencias de la Comunicación: con el fin de contribuir con el desarrollo de nuestro país y el binestar de la población.

VISIÓN :

Ser una facultad que se construya progresivamente en el tiempo; generando espacios que garanticen la formación de nuevos profesionales para satisfacer las necesidades del mercado con una aproximación a la excelencia.

1 Desarrollo del tema :

La Estadística es una ciencia formal que estudia la recolección, análisis e interpretación de datos de una muestra representativa, ya sea para ayudar en la toma de decisiones o para explicar condiciones regulares o irregulares de algún fenómeno o estudio aplicado, de ocurrencia en forma aleatoria o condicional. Sin embargo, la estadística es más que eso, es decir, es el vehículo que permite llevar a cabo el proceso relacionado con la investigación científica.

Es transversal a una amplia variedad de disciplinas, desde la física hasta las ciencias sociales, desde las ciencias de la salud hasta el control de calidad. Se usa para la toma de decisiones en áreas de negocios o instituciones gubernamentales.

La estadística descriptiva: se dedica a la descripción, visualización y resumen de datos originados a partir de los fenómenos de estudio. Los datos pueden ser resumidos numérica o gráficamente. Ejemplos básicos de parámetros estadísticos son: la media y la desviación estándar. Algunos ejemplos gráficos son: histograma, pirámide poblacional, gráfico circular, entre otros.

La estadística inferencial: se dedica a la generación de los modelos, inferencias y predicciones asociadas a los fenómenos en cuestión teniendo en cuenta la aleatoriedad de las observaciones. Se usa para modelar patrones en los datos y extraer inferencias acerca de la población bajo estudio. Estas inferencias pueden tomar la forma de respuestas a preguntas si/no (prueba de hipótesis), estimaciones de unas características numéricas (estimación), pronósticos de futuras observaciones, descripciones de asociación (correlación) o modelamiento de relaciones entre variables (análisis de regresión). Otras técnicas de modelamiento incluyen  series de tiempo y minería de datos

2 El tema 

ESTADISTICA  INFERENCIAL

  Definición:

• Es como sacar conclusiones generales para toda la población a partir del estudio de una muestra, y el grado de fiabilidad o significación de los resultados obtenidos.
•  Es una parte de la estadística que comprende los métodos y procedimientos que por medio de la inducción determina propiedades de una población estadística, a partir de una pequeña parte de la misma.

    Objetivo :

Generalizar las propiedades de la población, bajo estudio basado en los resultados  de una muestra representativa de dicha población.

Sin embargo los dos tipos de problemas que resuelven las técnicas estadísticas son: estimación y contraste de hipótesis.

En ambos casos se trata de generalizar la información obtenida en una muestra a una población. Pero antes de ello es necesario conocer el concepto de Distribución Muestral para conocer y entender los métodos y herramientas de la inferencia inferencial.

Distribución muestral: tiene por objetivo conocer el promedio de alguna característica cuantitativa o la proporción de individuos que poseen una característica cualitativa ejemplo: la edad media de los hombres que usan celular .

 Estas técnicas exigen que la muestra sea aleatoria.

Entre la muestra con la que se trabaja y la población de interés, o población diana, aparece la denominada población de muestreo: población (la mayor parte de las veces no definida con precisión) de la cual nuestra muestra es una muestra aleatoria. En consecuencia la generalización está amenazada por dos posibles tipos de errores: error aleatorio que es el que las técnicas estadísticas permiten cuantificar y críticamente dependiente del tamaño muestral, pero también de la variabilidad de la variable a estudiar y el error sistemático que tiene que ver con la diferencia entre la población de muestreo y la población diana y que sólo puede ser controlado por el diseño del estudio.

·       Tamaño muestral

Del mismo modo, para decidir el tamaño muestral: 

i) en un problema de estimación hay que tener una idea de la magnitud a estimar y del error aceptable. ii) en un contraste de hipótesis hay que saber el tamaño del efecto que se quiere ver.

1.   ESTIMACIÓN DE PARÁMETROS:

Con determinadas técnicas se realiza una predicción sobre cuáles podrían ser los parámetros de la población.

En general, de las variables experimentales u observacionales no conocemos pero  podemos conocer la familia (normal, binomial,...) pero no los parámetros.

Para calcularlos necesitaríamos tener todos los posibles valores de la variable, lo que no suele ser posible.

La inferencia estadística trata de cómo obtener información (inferir) sobre los parámetros a partir de subconjuntos de valores (muestras) de la variable.

Ø Estadístico: variable aleatoria que sólo depende de la muestra aleatoria elegida para calcularla.

Ø Estimación: Proceso por el que se trata de averiguar un parámetro de la población representado, en general, por  a partir del valor de un estadístico llamado estimador y representado por  .

El problema se resuelve en base al conocimiento de la "distribución muestral" del estadístico que se use.

¿Qué es esto? Concretemos  en la media (µ). Si para cada muestra posible calculamos la media muestral (x ) obtenemos un valor distinto (  x)es un estadístico: es una variable aleatoria y sólo depende de la muestra), habrá por tanto una  llamada distribución muestral de medias.

Con una muestra aleatoria, de tamaño n, podemos efectuar una estimación de un valor de un parámetro de la población; pero también necesitamos precisar un:

La desviación típica de esta distribución se denomina error típico de la media. Evidentemente, habrá una distribución muestral para cada estadístico, no sólo para la media, y en consecuencia un error típico para cada estadístico.

Si la distribución muestral de un estadístico estuviera relacionada con algún parámetro de interés, ese estadístico podría ser un estimador del parámetro.

1.1 Estimación puntual : es el valor obtenido del estadístico o estimador a partir de una muestra . es claro que para obtener la estimación puntual su valor dependerá de la muestra que se haya seleccionado y que el valor encontrado puede cambiar de muestra en muestral.De esta  manera las propiedades deseables serian que cada estimación no se encuentre muy alejada del verdadero valor del parámetro y por otra parte que no haya demasiada variabilidad entre los valores del estadístico ,obtenidos de muestra en muestra ,esto se puede formalizar definiendo algunas propiedades a tener en cuenta de los estadísticos a saber:

ü    Insesgado: informalmente esto significa ausencia de error sistemático. De una manera más formal un estadístico cualquiera q se dice insesgado si la media de su correspondiente distribución muestral es igual al parámetro de interés Q es decir E[q]=Q

ü    Eficiente: significa que las estimaciones obtenidas para distintas muestras varían poco entre ellas .de una manera más formal el estimador más eficiente dentro de un conjunto de estimadores insesgado será aquel que tiene la menor varianza.

ü    Consistente: informalmente un estadístico que se dice consistente si su variabilidad disminuye cuando aumenta el tamaño de muestra .

Se puede demostrar que la media aritmética es un estimador insesgado y eficiente de la media poblacional.si la variabilidad de las estimaciones se mide a través de la desviación estándar recibe el nombre de error estándar del estimador (SE).

1.2 estimación por intervalos:si bien la precisión se incrementa con muestras grandes no hay razón para esperar que la estimación puntual de una muestra dada deba ser exactamente igual al parámetro población que supone estima por ello existen muchas situaciones en las cuales es preferible determinar un intervalo dentro del cual se esperaría encontrar el valor del parámetro,teniendo en cuenta estos aspectos:

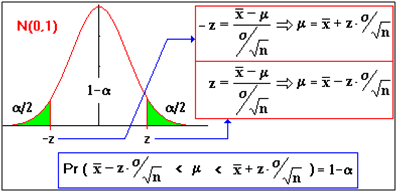
Intervalo de confianza: Se llama así a un intervalo en el que sabemos que está un parámetro, con un nivel de confianza específico.

Nivel de confianza: Probabilidad de que el parámetro a estimar se encuentre en el intervalo de confianza.

El nivel de confianza (p) se designa mediante 1 − α.

Error de estimación admisible: Que estará relacionado con el radio del intervalo de confianza.

1 2.  Contraste de hipótesis: Una hipótesis estadística es una asunción relativa a una o varias poblaciones, que puede ser cierta o no. Las hipótesis estadísticas se pueden contrastar con la información extraída de las muestras y tanto si se aceptan como si se rechazan se puede cometer un error. La hipótesis formulada con intención de rechazarla se llama hipótesis nula y se representa por H0. Rechazar H0 implica aceptar una hipótesis alternativa (H1).La situación se puede esquematizar:

	H0 cierta	H0 falsa H1 cierta
H0 rechazada	Error tipo I (a )	Decisión correcta (*)
H0 no rechazada	Decisión correcta	Error tipo II (b )

a= p (rechazar H₀|H₀ cierta) 
b = p (aceptar H₀|H₀ falsa) 
Potencia =1-0 = p (rechazar H₀|H₀ falsa)

Detalles a tener en cuenta

1. a y b están inversamente relacionadas.
2. Sólo pueden disminuirse las dos, aumentando n.

Los pasos necesarios para realizar un contraste relativo a un parámetro q son:

1. Establecer la hipótesis nula en términos de igualdad

2. Establecer la hipótesis alternativa, que puede hacerse de tres maneras, dependiendo del interés del investigador

en el primer caso se habla de contraste bilateral o de dos colas, y en los otros dos de lateral (derecho en el 2º caso, o izquierdo en el 3º) o una cola.

3. Elegir un nivel de significación: nivel crítico para a

4. Elegir un estadístico de contraste: estadístico cuya distribución muestral se conozca en H₀ y que esté relacionado con  y establecer, en base a dicha distribución, la región crítica: región en la que el estadístico tiene una probabilidad menor que a si H₀ fuera cierta y, en consecuencia, si el estadístico cayera en la misma, se rechazaría H₀.

Observe que, de esta manera, se está más seguro cuando se rechaza una hipótesis que cuando no. Por eso se fija como H₀ lo que se quiere rechazar. Cuando no se rechaza, no se ha demostrado nada, simplemente no se ha podido rechazar. Por otro lado, la decisión se toma en base a la distribución muestral en H₀, por eso es necesario que tenga la igualdad.

5. Calcular el estadístico para una muestra aleatoria y compararlo con la región crítica, o equivalentemente, calcular el "valor p" del estadístico (probabilidad de obtener ese valor, u otro más alejado de la H₀, si H₀ fuera cierta) y compararlo con a.

2.1Contraste bilateral

Se presenta cuando la hipótesis nula es del tipo H0: μ = k (o bien H0: p = k) y la hipótesis alternativa, por tanto, es del tipo H1: μ≠ k (o bien H1: p≠ k).

2.2.contraste unilateral 

3 vídeo 

4. Bibliográfia 

 
  . G. Hoel (1976). Estadística Elemental. Editorial Cecsa. México.

  . Parsen E. (1973) Teoría Moderna de Probabilidad y sus aplicaciones. Editorial Limusa. México.

  . Nolberto V. (2008) Estadística Inferencial Aplicada. Editorial de la Unidad de Post grado de la Facultad de    Educación de la Universidad Nacional Mayor de San Marcos. Lima, Perú. 

5.Anexo